GRADIENT DESCENT

GRADIENT DESCENT:

 
It is an optimization technique which helps us to find the values of parameters(coefficients) of a function (f) that minimizes the cost function(cost).

The word Gradient means slope and Descent means downward. We will decreases our slope in cost function to find the optimal value of the coefficient 

It is best used when the parameters cannot be calculated analytically(means by linear algebra) and must be searched for by an optimal algorithm. 

Intuition of Gradient descent:

Let's consider a bowl in which you eat cereal or store fruit in. The bowl is a plot of cost function(f).

A random position on the surface of bowl is the cost of the values of the coefficient(cost).

The bottom of the bowl is the cost of best set of coefficients, the minimum of the function which is also known "Global Minima".

Our main goal is to find the global minima point on that curve which will give us the best values of the coefficients. 


Basically there are two type of minima:

1. Global minima:- It is the least minimum points of  our cost function for which we are calculating our values. There is only one global minima. 

2. Local minima:- It is not a least minimum point in the cost function. There are many local minima's.


So, don't get confused with the local and global minima. Our motive is to find the minimum point in our function which is Global minima.

In this article we are gonna understand the gradient descent technique for linear regression.

As we all know that the MSE(Mean Squared Error) of regression line is :



When we calculate our gradient descent, the MSE function is equal to our cost function.

MSE = Cost function

Cost function can also be written as the function of slope(m) and intercept(c) :-


"" I have change the function from "f(m,b)" to "J" and intercept  "b" to "c", for some calculation purposes. Use can use any letter and variable you want to display the cost function. ""

 

Our main motive is to find the best value of m and c, such that our error rate is minimum.


Firstly we will differentiate our cost function w.r.t slope(m).

 

Now differentiate cost function w.r.t our intercept(c).



Forming 2 equation of slope m and intercept c.



Here, 





 λ is parameter which is adjusted according to the best value of m and c for which error rate is minimum.

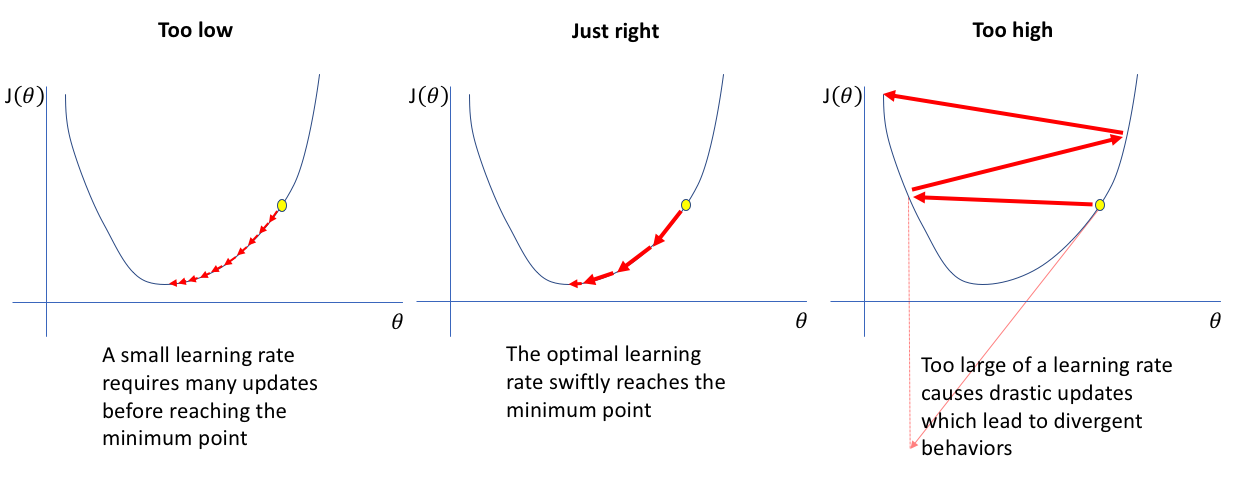
For low, right and high value of   λ :


 

Steps to find the best value of slope(m) and intercept(c) 

Firstly we assume our m and c value as 0. By assuming the values as 0, the equation of m and c are the worst values for which error rate is high. Now, change the value of learning rate and update in the equations of m and c. Repeat the process until we find the minimum value of our error rate. 



That's how the Gradient descent works in Linear regression.

THANK YOU! 😀😀


Check out my another article :


 


Comments

Post a Comment

Popular posts from this blog

Stochastic gradient descent Intuition

Image
  T his is a part 2 of my blog on the optimizers. Previously I had explained about the Gradient Descent which is the basic building blocks for the other optimizers, if you want a revision check out my previous article. Link is in the bottom of this article. SGD :-   It is a similar type of optimizer as Gradient Descent, but the main difference is that it only runs for one data point at a time. Let me explains a little bit more. When we use our Gradient Descent, we take all the data points, do the iteration for number of the epochs we assigned and compute our loss function. But in the SGD we only take one single random point and compute the loss function for every epochs. The main advantage of the SGD over the Gradient Descent is that it is less time computational and less expensive. In SGD we only use one data point, due to this some noise occurs while finding our global minima. To remove these type of noise we use the concept of Momentum .  SGD with Momentum :-  As,...
Read more